What would happen if we had no leap days?

Hello, this is Ivan, team lead developer here at Datawrapper. Last Saturday was 29th February – a leap day. This got me thinking about what would be different if we had no leap days, so today we’ll take a look at this hypothetical scenario.

The Gregorian calendar is the most widely used in the world^[1] . Normally a year in this calendar has 365 days, but in a leap year there are 366 days, with an extra day added on 29th February.

But what if we all used the same version of the calendar, except that we wouldn’t add any leap days? Let’s call this imaginary calendar the No-leap calendar.

I visualized this thought experiment by plotting the seasonality of a normal Gregorian calendar year against seasonality of a No-leap calendar.

While 5th March 2020 (the day this Weekly Chart got published) is the start of spring in the Gregorian calendar, the same date would, in fact, be around the middle of autumn in the imaginary No-leap calendar.^[2]

So how is it possible that the same date could be in two different seasons? That’s because 5th March 2020 in a normal calendar is not the same as 5th March 2020 in our imaginary one.

For the No-leap calendar, we assume that no leap days ever occur. To establish the difference in dates that this would lead to, we need to trace the starting point of the Gregorian calendar and know when leap days occur.

Starting point

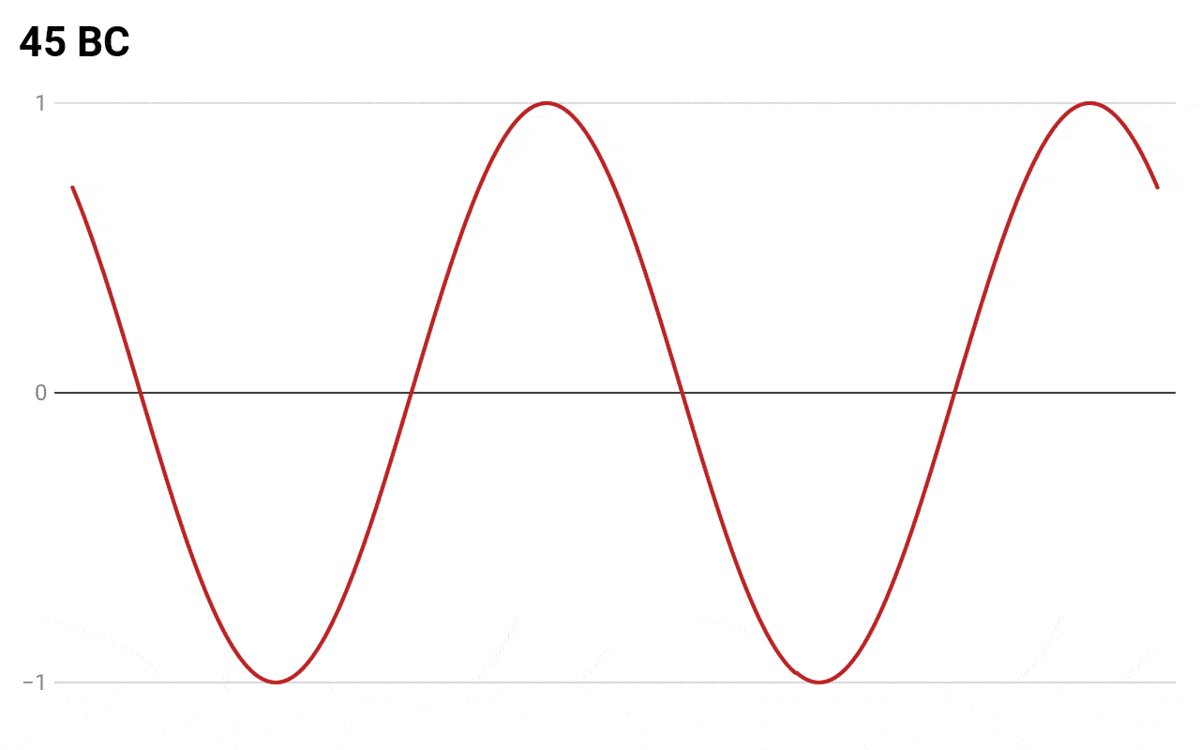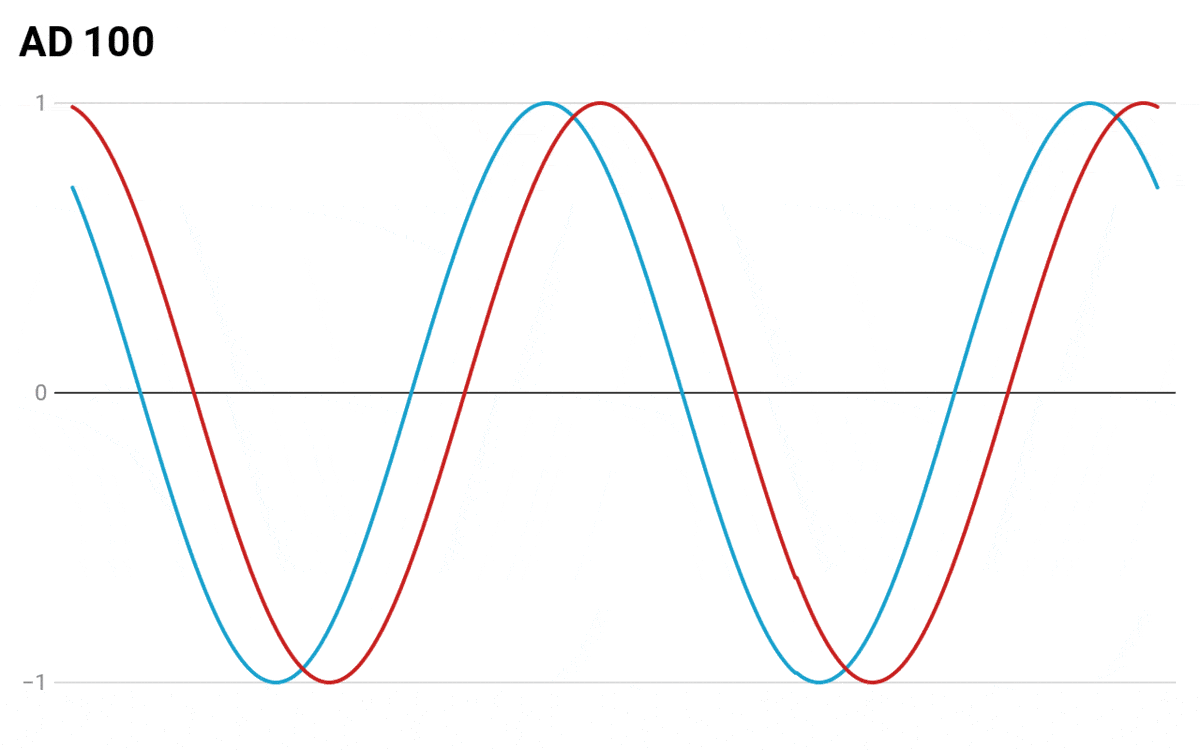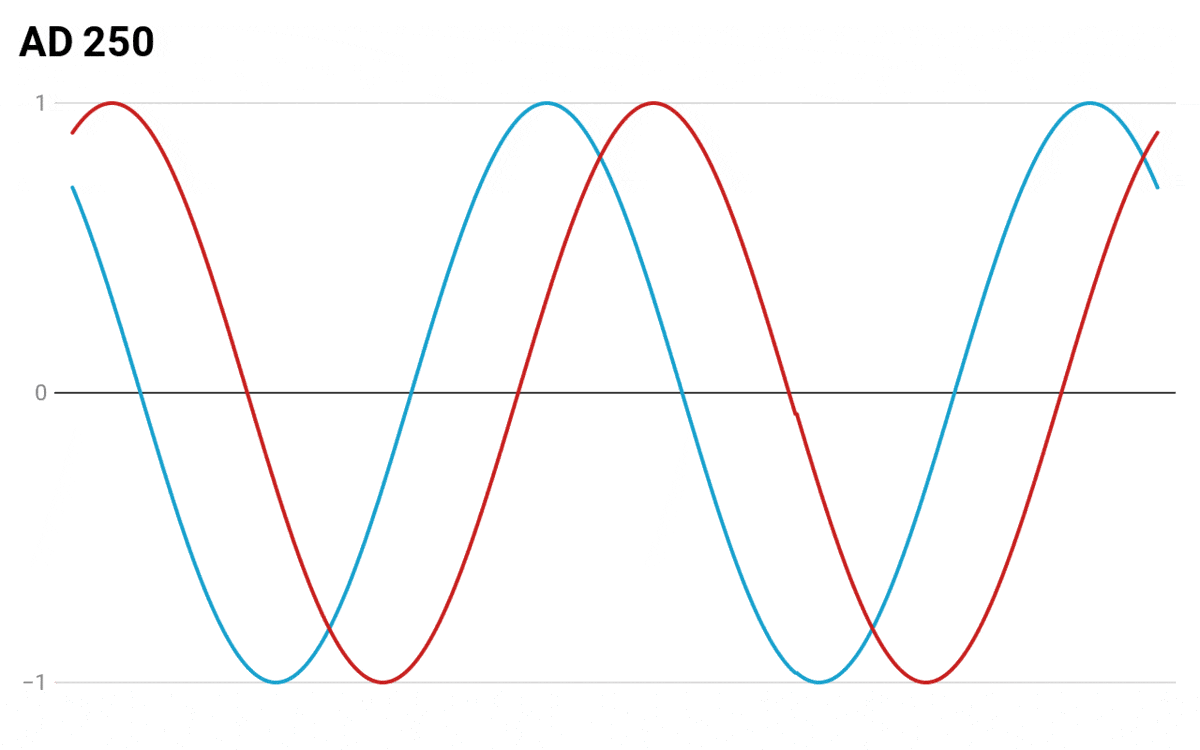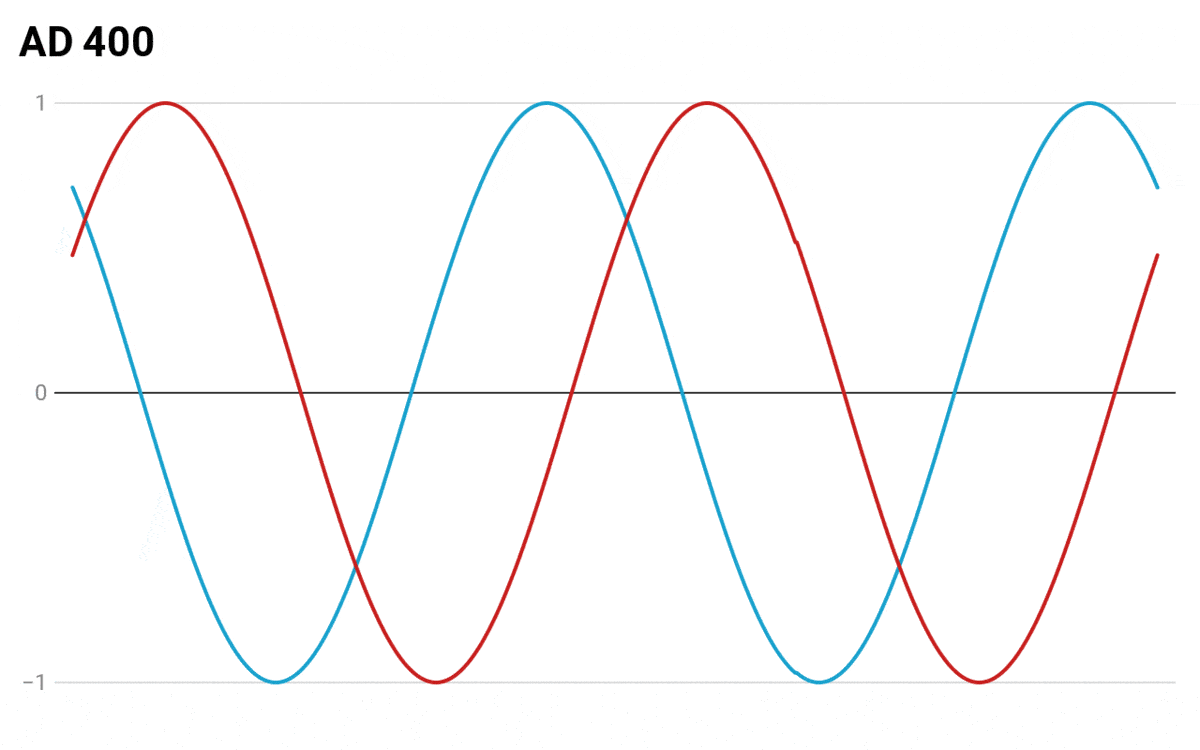
The Gregorian calendar was first adopted in 1582 and is itself a correction to the Julian calendar which was adopted in 45 BC. So when I make a comparison between the calendars in the chart, I use 45 BC as the starting point at which the two calendars start diverging. From this point, one of them has leap days and the other does not.

Leap days

In the Gregorian calendar, leap days account for the fact that an average year is approximately 365.2422 days long.

The rules for determining whether a year is a leap year are as follows:

A year is normal unless it is evenly divisible by 4 in which case it is a leap year. For example:

2020, 2016 and 2012 are leap years (divisible by 4) 2019, 2018 and 2017 are normal years

An exception to this rule is a year that is evenly divisible by 100, in which case it is NOT a leap year, unless it is also evenly divisible by 400, in which case it IS a leap year. For example:

1900, 1800 and 1700 are normal years (divisible by 100) 2000, 1600 and 1200 are leap years (divisible by 400)

It can be a bit tricky to get your head around this. If you would like to learn more about which years are leap years, have a look at this article.

---

So now we can calculate how many leap days the No-leap calendar would have missed up to today in comparison to the Gregorian calendar:

2065 years and 65 days have passed since the start of 45 BC until 5th March 2020 in the Gregorian calendar. This amounts to 754290 days in total if we account for all the leap days (I was lazy, so instead of calculating it by hand, I used a JavaScript library called moment.js to do it for me).

To now calculate the date in the No-leap calendar which corresponds to 5th March 2020 in the Gregorian calendar, we divide 754290 by 365 (a stable number of days in a year that never changes) with remainder and get 2066 years and 200 days. This is how far ahead the No-leap calendar is, since it didn’t have any leap days.

So 5th March 2020 would actually be 20th July 2021 in the No-leap calendar! This is kind of mind-bending. But it explains the disparities in seasons when you look at the same dates in different calendars. If you take a look at the chart above again, you will see that 20th July 2021 in the No-leap calendar is at exactly the same point in season (start of spring) as 5th March 2020 in the Gregorian calendar.

Seasonal drift

To help visualize how the seasonality in the two calendars deviate from each other as time passes, I made an animation which shows how the drift in dates occurs starting from the year 45 BC:

Notes and chart choices

To visualize seasonality I used abstract “season values” where 1 denotes the peak of summer and -1 denotes the peak of winter. At first, I considered using some real measures like the amount of daylight or average temperature, but since the chart was designed as a thought experiment and for the sake of simplicity I settled on using these simple values.

The downside of using such season values is that you need both the value and the current trajectory to know what part of the season a value corresponds to. For example, a value of 0 corresponds both to middle of spring and middle of autumn. The former occurs when the trajectory is going up and the latter when the trajectory is going down.

I used 15th July as the normal peak of summer and 15th January as the normal peak of winter as these dates correspond to the meteorological seasons of:

• spring that lasts from start of March until end of May
• summer that lasts from start of June until end of August
• autumn that lasts from start of September until end of November
• winter that lasts from start of December until end of February

To produce the seasonal lines I calculated the difference in days between the two calendars for each given date and mapped seasonality onto it.

Instead of using a linear progression where the seasonal values go up and down in a straight line, I wrote a script that produced the data to appear as sine waves. I think it represents the non-linear changes in seasons better (and it also looks cooler🙂).

One more thing to note: It’s difficult to determine the real starting point of the original Julian calendar and how it relates to the changes made in the Gregorian calendar. We can’t fully rely on this information being accurate, but for the sake of this thought experiment, picking a certain starting point and sticking to it for all calculations works fine.

---

I hope you enjoyed this Weekly Chart! I certainly learned a lot about leap days while making it. Let me know in the comments or on Twitter if you have any questions. We’ll see you next week!

1. Many other calendars exist, but for the sake of convenience most societies use or at least recognize the Gregorian one. ↩︎

2. When I refer to different seasons, I’m specifically talking about seasons as they occur here in Berlin and other places in the Northern hemisphere. In the Southern hemisphere, seasons are often reversed (winter in July, summer in January) and there are many places with different seasonal patterns altogether, such as only a wet and a dry season. Besides, seasonality is subject to change for various natural and human-made reasons. ↩︎