How to measure the Earth

Hello, Rose here. Today I’m excited to introduce a new regular blog series: Map Stories.

Many of you already know Datawrapper’s cartographer, Anna, who creates the basemaps that underlie all our choropleth and symbol map offerings. Whether you’ve met her in our support inbox or through one of her Weekly Charts, you know that Anna loves maps — and knows a ton about them. She’s already shared that knowledge in many posts on the blog, especially ones about maps of natural and historical events (from crane migrations and volcanic eruptions to ancient warfare and North Pole expeditions.)

But there’s a lot more to say about maps! Which is to say, about the Earth itself and all the ways we humans have tried to measure it. So we’ve decided to make Map Stories a regular format, where Anna (and maybe others) will be writing about maps and mapping more often.

Today’s story starts with a fundamental question: How big is the world?

Here’s Anna...

---

In my day-to-day work at Datawrapper, I encounter geographic data in various formats, using different projections and systems of measurement, from a number of different sources. There are lots of equally good “spatial reference systems” for making maps, and since they all describe where things are on Earth, they’re not as different as they might seem. One crucial parameter in all modern reference systems is the circumference of the Earth.

The first known calculation of the Earth’s circumference was made 2300 years ago by a man called Eratosthenes. I remember in school, how impressed I was by how accurately the Earth’s circumference was measured such long time ago. Today we’re going to take a closer look on how his calculation was made.

Eratosthenes was born in Cyrene, Libya in 275 BCE and is considered the father of scientific geography. At the age of 35, he was invited by Ptolemy II to become the chief of the library in Alexandria, which at the time had become a center for geography. Eratosthenes was the author of several books, but there are only a few fragments left of the original works — what we know about his calculations comes from a summary written over 400 years later by the Greek astronomer Cleomedes. And of all of Eratosthenes’ contributions to scientific geography, by far the most famous was his attempt to measure the magnitude of the Earth.

In his time, the idea of the Earth as a sphere had already become generally accepted. That meant that geometrically, the method to calculate its circumference was a simple matter of proportion. If you chose the right two places to measure from, then:

Let’s see how this proportion works.

How to choose two cities

The circumference of a sphere is the length of the biggest possible circle that can be traced around it. Any circle that passes through two exactly opposite points on the sphere is as big as possible and is known as a “great circle.”

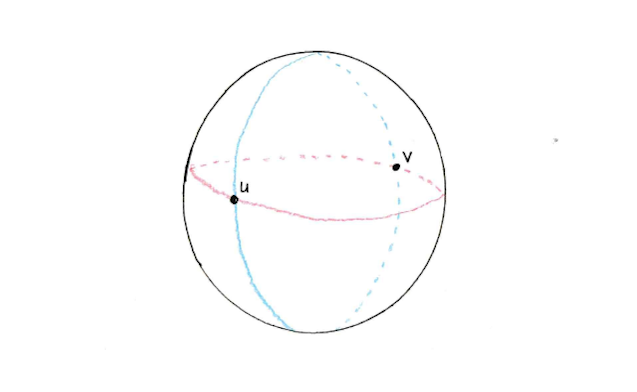
In geography, each line of longitude is a great circle, since it passes through both the North and South Poles — so when two cities are on the same longitude, the distance between them is a fraction of that great circle. If you knew how far apart they were in latitude, you’d know exactly what fraction that was.

How to measure the difference in latitude

At Eratosthenes’ time, it was the general belief that Syene was located on the Tropic of Cancer. That’s the latitude where, on the summer solstice, the sun passes directly overhead. Its rays shine straight down on the Earth and objects don’t cast any shadow.

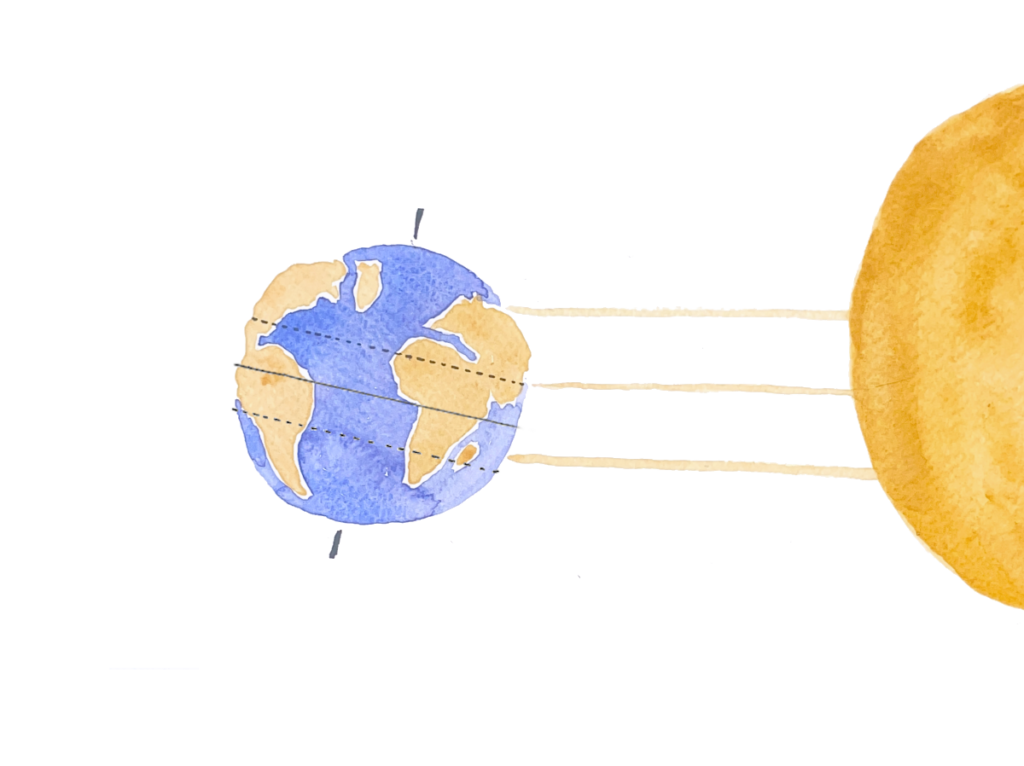
Because Alexandria is north of the tropic, the sun passes over it at an angle even on the summer solstice. In this sketch, I labeled that angle α. The rays that shine on Alexandria are parallel to the sunshine over Syene, so that same angle is also the difference in latitude between the two cities.

To observe the angle of the sun, Eratosthenes used a scaphe, a type of sundial that has the shape of a bowl with degrees marked out and a stick in the inside that casts a shadow. In Syene, the stick would not cast any shadow at noon on the summer solstice, but in Alexandria, the angle of the shadow was measured to be 7.2 degrees.

How to measure the distance

While we can be relatively sure how Eratosthenes measured the difference in latitude, the method of measuring the terrestrial distance between Alexandria and Syene is not as clear. It might have been measured by caravans or bematists, professional surveyors who measured distance by pacing. We do know that the distance used in his calculation was 5000 stadia (a Greek unit of length).

Putting the measurements into the equation, we get:

Eratosthenes’ assumptions weren’t 100% accurate…

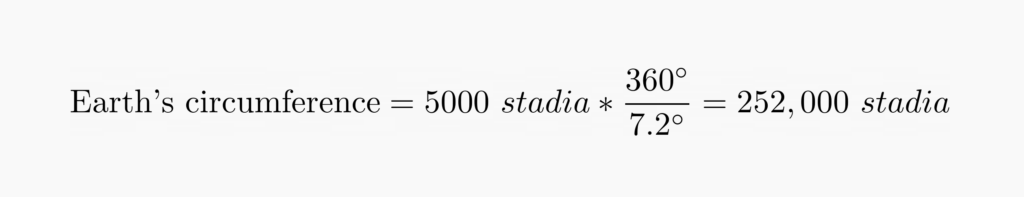
Eratosthenes counted on two assumptions: that Syene was on the Tropic of Cancer, and that it was on the same longitude as Alexandria. Today we know that Syene is actually 3° east of Alexandria’s longitude, and at the time of the observation it was also not quite on the Tropic of Cancer (the location of the tropics are not constant — they shift over the years due to the undulation of the Earth’s axis!)

…but he still made an incredibly good estimate

Eratosthenes calculated the Earth’s circumference as 252,000 stadia. Some historians believe that this figure is not a coincidence, since it can be divided by all numbers from 1 to 10, which makes other calculations easier. One theory is that Eratosthenes actually redefined the stadion based on his measurement of the Earth.

Either way, we know for sure that no universal definition of a stadion existed, and we don’t know exactly which definition Eratosthenes used in his calculations. A stadion can be 157-209 meters. The error of his estimate varies depending on which definition is used when converting stadia to meters: Assuming that one stadion is 185.3 meters (according to the Ptolemaic definition), 252,000 stadia corresponds to 46,695 kilometers — and the value we know today is 40,008 kilometers around the Earth. Even if there are a few sources of error, Eratosthenes’ measurement is only around 5% off from the true value. Mind blowing, isn’t it?

---

Thanks for reading the first post in this new series. Stay tuned for the next Map Story. Until next time!