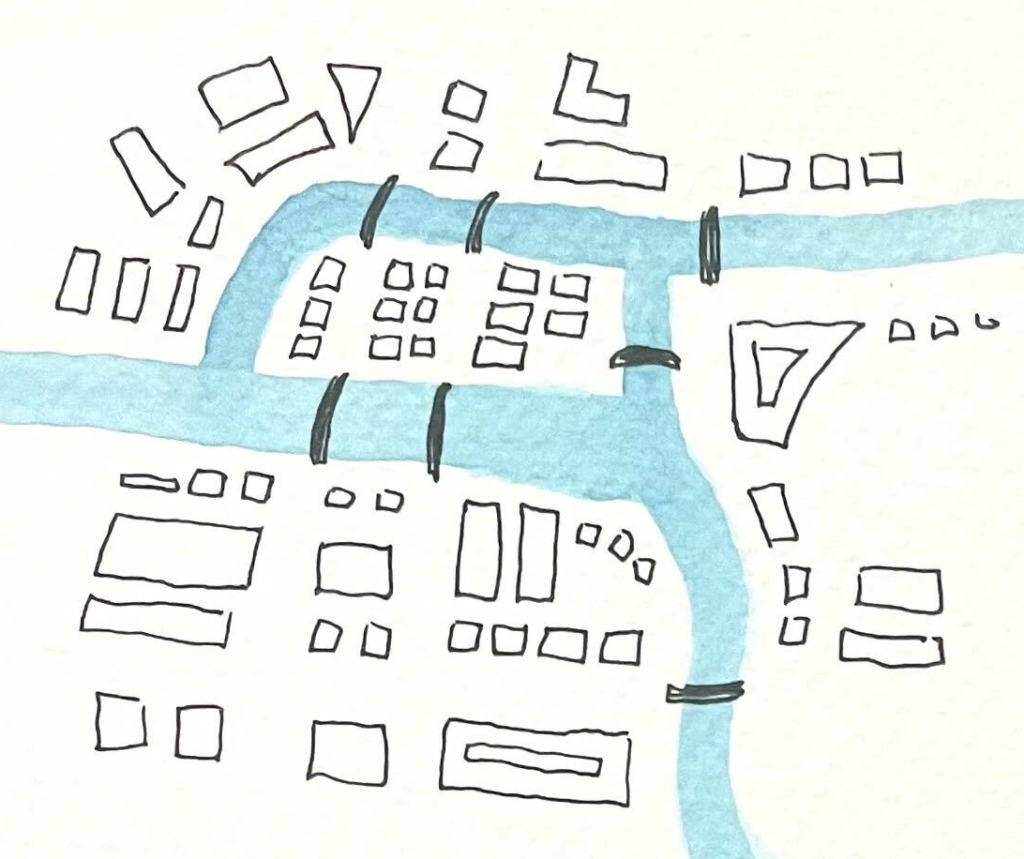
What happened to the seven bridges in Königsberg?

Hi everyone — I’ll be taking a leave from work this year so Map Stories will take a break for a while too. See you again in spring 2025!
In the last map story, about a transit map from ancient Rome, I briefly mentioned the mathematician Leonard Euler and a discovery he made about the city of Königsberg and its seven bridges.
According to mathematical legend, the citizens of Königsberg invented a game when going for Sunday walks in the city. The game was to find a route that crossed all seven bridges over the river Pregel, without crossing any of them more than once. This trivial Sunday game puzzled Euler, and his efforts to prove that no such route exists led him to develop the foundations of graph theory, a completely new field in mathematics. Today, this type of route is called an Euler walk.
But what happened to the bridges in Königsberg after Euler formulated the problem in 1735?
A bridge history of Königsberg
Königsberg was founded in 1255, where the river Pregel flows into the Baltic Sea. In Euler’s days, the city was the capital of Prussia, a province of the Holy Roman Empire. After the dissolution of the Holy Roman Empire, East Prussia and Königsberg became a part of the German Empire in 1773, and later the Weimar Republic. Under the Potsdam Agreement in 1945, the city came to belong the Soviet Union and changed its name to Kaliningrad.
The city was heavily bombed during WWII, first by the Soviet Union in 1941, then by the British in 1944. Almost 80% of the city was destroyed by the bombing, including several of the bridges:
Would an Euler walk be possible today?
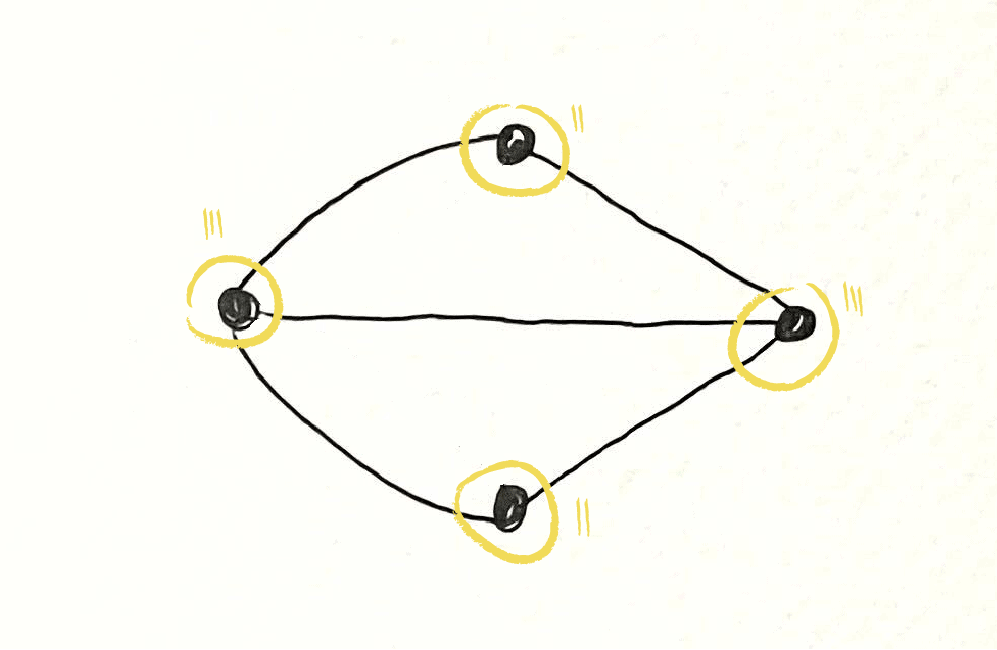
What made Euler's solution so famous was that he formalized the problem in an abstract way. He removed all features of the landscape except the land masses and bridges, and considered the land masses as vertices and bridges as edges connecting them. This type of diagram is called a graph.
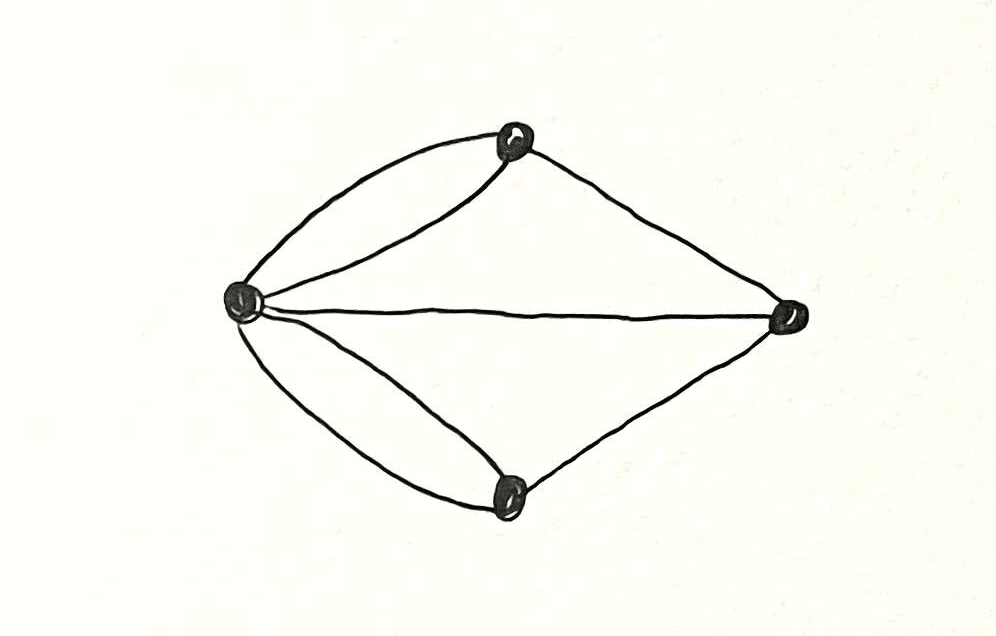
The properties of a graph depend on how many vertices it has and how the edges connect them. In this case, Euler proved that an "Euler walk" is possible only if the graph has exactly zero or two vertices of an odd "degree."
The degree of a vertex is the number of edges that connect to it — in other words, the number of times it can be entered or exited. (Remember that in an Euler walk, if a vertex is entered from one edge, it has to be exited by another — we can't cross any bridge twice.) If any vertex has an odd number of connecting edges, then the last time we cross a bridge to enter it, we'll have no bridge left to leave it by. There's only two places where that's all right: the starting point of our walk, which we can exit without having to enter, and the ending point, which we can enter without having to exit.
In the graph of Königsberg from 1735, all four vertices have an odd number of connecting edges:
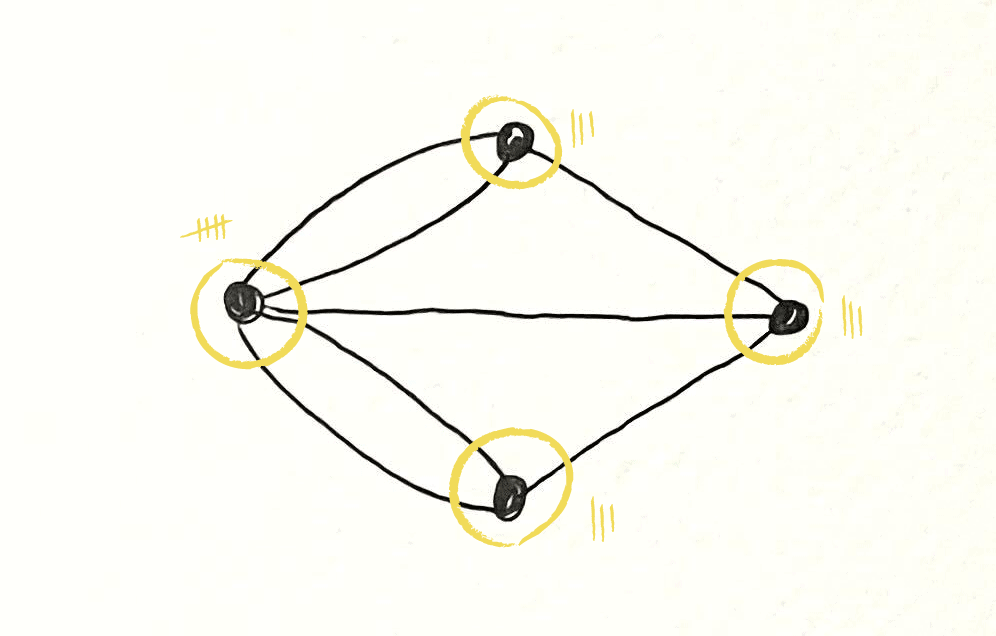
But with only five bridges left in Königsberg, today it is actually possible to find an Euler walk through the city. The graph has only two vertices of odd degree, so it's possible to cross all of the city's bridges without crossing any of them more than once. Can you see how?
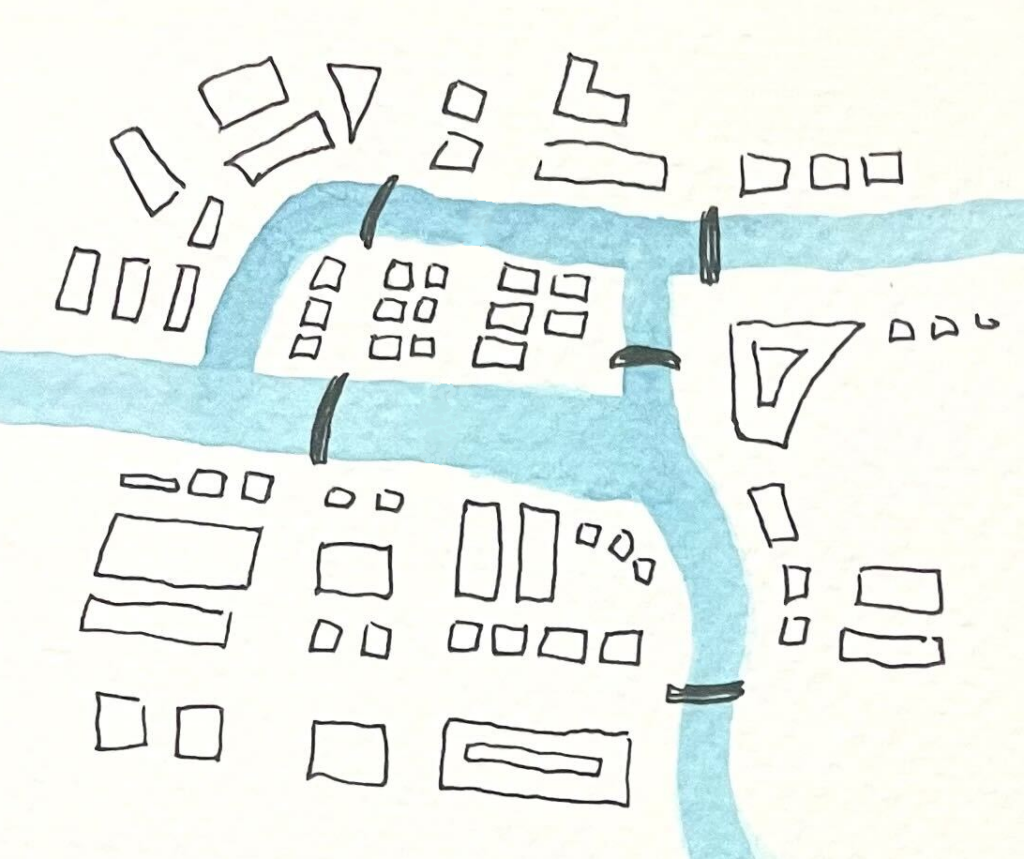
Graph theory has a great importance in many fields of science, including computer science, chemistry, biology, and linguistics, where graphs are used to model all kinds of relations, networks, and processes.
What if this route had already been possible in Königsberg in the 1700s? If Euler hadn't been puzzled by the walking problem, maybe he wouldn't have been pushed to create this completely new field of mathematics?
We'll see each other for more Map Stories next year!




Comments